HORIZON OF COGNITION
The next figure shows the dependency of a measurable interval in relation to its real size in a curved space. This dependency generally applies both to macro and micro areas. An interval can be understood as anything we can quantify – what we perceive, measure, evaluate, i.e. anything in our world. Therefore, it concerns mathematics, physics, astronomy, psychology, philosophy, etc.
The following figure implies the importance of the axis origin – the point where the interval starts – the position of the observer.
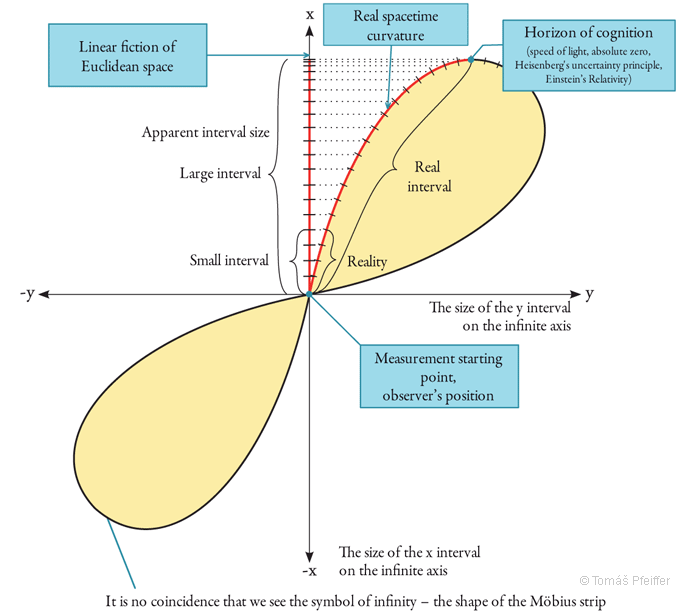
Figure 2 – Horizon of cognition
In practical terms, when moving in any direction following a straight line, since it is curved, we always return in an infinite circle to the position of origin. For example, in spacetime this is manifested by the existence of archetypes (everything has already existed, and always in a slightly different way). This means there is a finite amount of processes in their infinite variety. I would like to expand the idea in a future book, as well as the manner in which to perform a change in the observer so as to go beyond the horizon of cognition.
The shape of the curve likely demonstrates the matching frequency of similar to identical processes and states, and thus depicts the horizon of cognitions in another way.
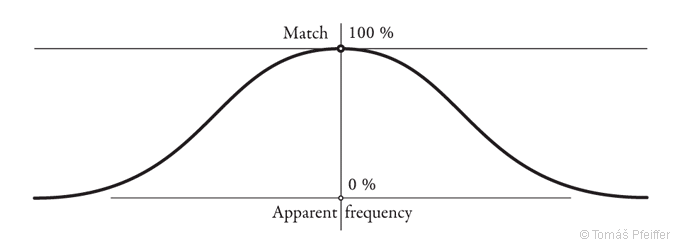
Figure 3 – Gaussian curve
This had already been understood and put into practice by Indian rishis, the authors of the oldest written records which are 7 to 20 thousand years old. It is one of the greatest mysteries of the palm leaves libraries that rishis and their disciples wrote thousands of years ago for next generations as well as for our contemporaries. The records sometimes include completely accurate information. Hence they substantially shift our understanding of causality. This has a close connection with the horizon of cognition and interpretation of destiny.
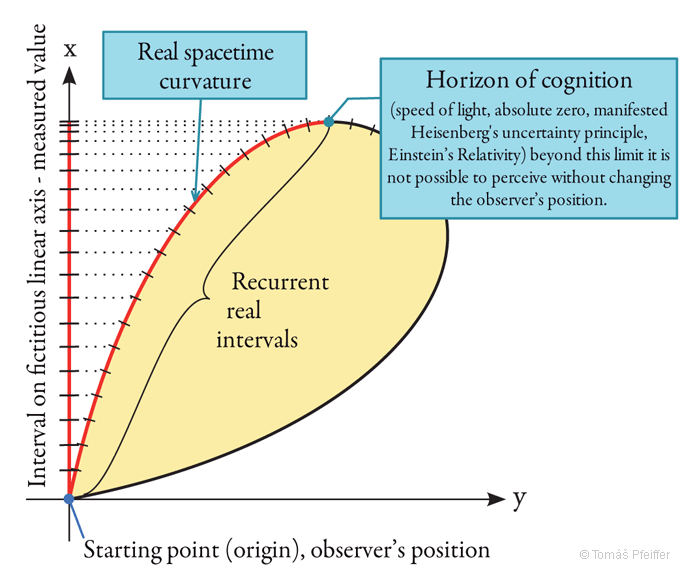
Figure 4 – Schematic illustration of the horizon of cognition
Problems of today’s mathematics of infinity, physics, astronomy, etc., are associated with the phenomenon depicted above in Fig. 4. A paradox arises as the measured spacetime is in principle considered linear, while we talk about relativity and not include it in the equations describing those areas. We must remember that any system of XYZ axes or grids is only our concept in an attempt to grasp an interval; for instance, the actual placing of the starting point in a space does not, in any way, affect the measured value itself relative to this point.
Nonlinearity is also manifested in the fact that any attempt at measurement is burdened by error being infinitely small at small intervals and, conversely, infinitely large at large ones. When in proximity to the horizon of cognition, no matter how large the interval in the curved spacetime is, it no longer increases the interval on the fictitious linear axis. This is what I call the horizon of cognition beyond which it is not possible to observe, i.e. measure, anything anymore. It is always true for both directions – towards the universe and the atom, i.e. for light-years and angströms.


