Chapter 3
The micro world
3.7 Matter is energy, energy is vibration
We have previously shown how spacetime quantisation results in wave manifestations of particles, that is the relation particle → wave. But is it possible for the opposite to apply as well? Could the relation wave → particle exist if quantised spacetime behaved and manifested itself the same way as a particle? Would it not make it possible to explain, say, the behaviour of photons – i.e. quantum particles with zero rest mass?
In order to follow these thoughts, we must first consider the essence of matter and energy again.
Josef Zezulka discusses this in the chapter “Matter is energy, energy is vibration” in Lectures II. [2], appendix 1, page 51–52:
„Let’s imagine that we are able to observe matter in such a way that our observation takes us to incredible depths. This is only an image, which could be real if humans had the right knowledge and technical possibilities. We already know that matter is made up of atoms. This image is similar to that of a starry sky. There are fixed stars, planets etc., like in the macro cosmos. (...) If we observed it more deeply, atom particles would appear as energy. And energy, in its vital manifestation, would appear as vibrations.“
Philosophical observations of the micro world provide us with two views. One is fractal and shows a structure that repeats itself infinitely below (and above) us. The other view perceives energy–vibrational manifestations of the micro world, and from our point of view they are just as valid and real as the fractal view.
We can thus regard matter as the “fundamental building material for everything that we perceive as reality” ([2], appendix 1). It is building material not only for visible matter but also for its force effects, observed in a sequence of time.
Both views are simultaneously valid and bring us closer to understanding the terms matter and energy.
Is it already possible for us to observe the energy-vibrational character of particles? In 2007 a team from the Swedish university Lund published the first images of a dynamic electron motion on an electromagnetic wave [42]. In order to record this, innovative stroboscope setup was developed. It combines two synchronised lasers (one generating extremely short ultraviolet attosecond (10−18 s), pulses, which ionised atoms and temporarily localised their electrons; the other laser generated infrared pulses controlling their dynamics). This made it possible to get an image of a moving electron (more specifically its corresponding localised wave packet). The film showing this phenomenon can be found at [43]. The results were compared to the numerical solution of the corresponding Schrödinger’s equation, and the data from the experiment and the calculations showed an excellent agreement, which is shown in Fig. 3.5.
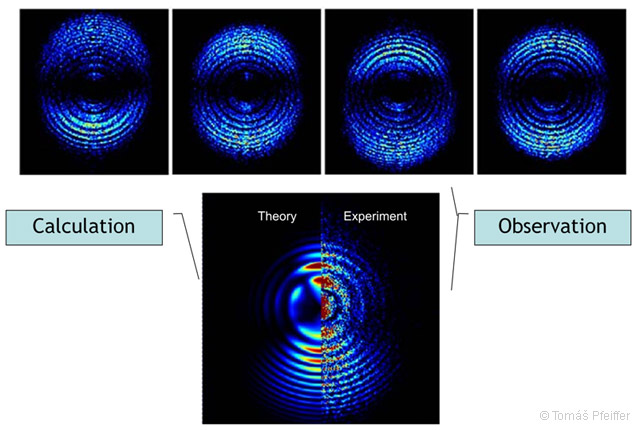
Figure 3.5: Observation of the dynamic (location change in time) of a localised electron and a comparison with the solution of the wave equation. Published by the team at Lund University, Sweden [42].
Johan Mauritsson, a member of the team at Lund University commented: „It takes an electron about 150 attoseconds to orbit the nucleus of an atom. One attosecond lasts 10−18 s, and if we draw out one attosecond to the length of a second, it would be like drawing out a second to the age of the universe.“ [44]
The image does not picture the electron as a planet in a sub-universe; it shows the distribution of its energy state (wave packet), which agrees with the corresponding calculations of quantum mechanics. Does it not remind you of drop of water that has hit the surface?
The research presented above is closely related to a new and interesting view of our current understanding of matter and energy that was introduced by Jeff Yee [45] namely the Energy Wave Theory [46]. This theory considers matter particles to be standing longitudinal waves localised at so called “wave centres” (as Yee points out, these are very similar to the observations made by the Swedish scientists). Matter (rest mass) is determined by energy deposited in these standing waves:
m0 = E/c2 (3.3)
where m0 is the particle rest mass, E is the energy of the corresponding standing wave, and c is the speed of light in a vacuum.
The equation (3.3) is based on Einstein’s famous equation (E = mc2), and defines the rest mass of a particle as the energy of the corresponding standing waves divided by the speed of light squared. An illustration of this view of a particle is shown in Fig. 3.6.
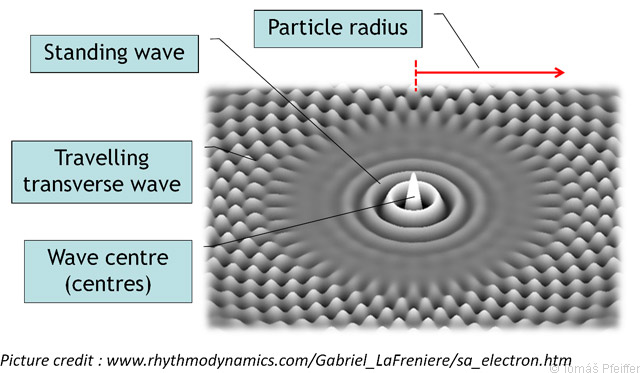
Figure 3.6: A schematic image of a particle depicted as energy deposited in a form of standing (longitudinal) waves [46]. Waves are actually longitudinal. We can picture the waves with the help of a small ball and a sphere. Imagine a small ball (the wave centre) in the middle of a closed sphere filled with air (the entire particle). If we quickly deflate and inflate the ball, standing longitudinal waves would form inside the sphere.
Energy quanta (photons) are then described as travelling transverse waves, which originate as a consequence of the oscillations of matter particles (all matter with a temperature higher than absolute zero always emits heat radiation). According to this theory, energy is understood as being the motion, waves of the universe, which can be used to describe all known interactions, attractive and repulsive forces. The Energy Wave Theory hence assumes the existence of an omnipresent aether (a medium that has its own density), representing a system of interconnected grains/granules that transfer energy. Wave centres (which can be used to describe the particles of matter) are then able to reflect, absorb or emit this energy (which changes their energy state in the given system, e.g. an atom).
The Energy Wave Theory gives remarkable outputs and provides a simple explanation to many observations in particle physics. For example, it is able to describe all known particles and antiparticles as combinations of a single fundamental particle (representing the previously mentioned wave centre) and it also lowers the number of fundamental physical constants significantly (from more than 20 to a mere 5) [47]. This is very significant because every empirically determined physical constant sets a limit (horizon) on our understanding of the natural law it helps describe. It is an expression of our inability to understand further. More knowledge and a deeper understanding of natural laws should hence entail lowering the number of fundamental physical constants.
Read more >>

