Kapitola 3

Mikrosvět

3.1 Duální projevy kvantových mikročástic při dvouštěrbinovém experimentu

Dualitou částice a vlnění se zabýval francouzský kvantový fyzik Luis de Broglie, který navrhl princip duality částic a vlnění [31], za což dostal v roce 1929 Nobelovu cenu [32].

Podle tohoto principu lze popsal vlnové vlastnosti částic rovnicí:

λ = h/p = h/(mv)       (3.1)

kde λ je vlnová délka, h Planckova konstanta, p hybnost, m hmotnost částice, a v rychlost pohybu částice. Při vysokých rychlostech pak za hmotnost m dosazujeme hmotnost relativistickou.

kde m₀ je klidová hmotnost, v rychlost a c rychlost světla ve vakuu.

Pozn.: Jak je všeobecně známo, samotná kvantová mechanika je nerelativistická. Pouze při popisu relativistických částic se kvantová mechanika rozšiřuje o speciální teorii relativity a vznikne tím Kvantová Teorie Pole (Quantum Field theory) což je plně relativistická teorie. Také se to nazývá “Druhé kvantování”. Zatím se však nepodařilo zformulovat teorii, která by zahrnovala jak projevy kvantového světa, tak i gravitaci.

Kvantová mechanika ve své základní podobě nepracuje s pojmem časoprostor. V předchozím povídání jsme si však zdůvodnili, že je to právě kvantovaný časoprostor, který stojí za výše uvedenými vlnovými projevy mikročástic.

Zopakujme si, že při pozorování objektů na horizontu poznání směrem do mikrosvěta se v našem pozorování časoprostor rozpadá na množinu vzájemně propojených (nerozpojitelných) intervalů, ve kterých má nutně každý z nich i svouzápornou protiváhu. Ty se pak staví za sebe a částice v našem pozorování kmitá mezi nimi (pro nás existuje zároveň ve všech možných výskytech).

Tyto intervaly se u pohybující se částice šíří v prostoru jako vlna, přičemž její vlnová délka vyjadřuje zakřivení časoprostoru na horizontu poznání. Můžeme tedy mluvit o rozvlnění samotného časoprostoru, které je důsledkem (projevem) našeho pozorování.

A tak si ve dvouštěrbinovém experimentu můžeme představit situaci, kdy vyšleme pouze jednu jedinou částici. V naší modelové představě (objekt na hranici horizontu poznání) se bude jednat o bod (kvantum) s nenulovou klidovou hmotností.

V našem pozorování však již nemůžeme mluvit o částici, ale o „projekci časoprostorové neurčitosti bodu“, šířící se časoprostorem. Toto je schematicky znázorněno na obr. 3.1.

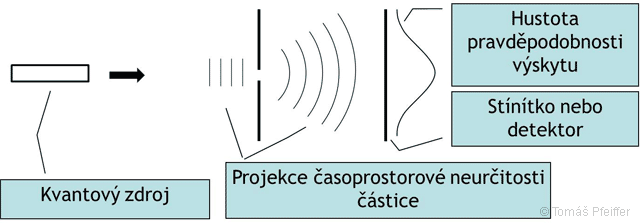
Obrázek 3.1: Pohyb cástice na horizontu poznání. Ze zdroje vyšleme pouze jednu jedinou cástici, která je pro naše pozorování blízko horizontu poznání. Pokud cástici experimentálne nijak nemeríme a neomezujeme jde o volnou cástici, která se nerozlišitelne vyskytuje/šírí v množine vzájemne propojených casoprostorových intervalu (strídají se intervaly s kladnou i zápornou polaritou). Pokud cástice projde úzkou šterbinou, jsou vlnoplochy takto vzniklé vlny v našem prumetu kruhové.

A teď takovému útvaru postavíme do cesty přepážku se dvěma štěrbinami.

Z důvodu nerozlišitelnosti (nepoznatelnosti) způsobenou horizontem poznání pak pozorujeme interferenci tedy skládání jednotlivých „vln“ z obou štěrbin (inu částice se ve vzdáleném pozorování může vyskytovat jen v takových pozicích, ve kterých nepoznáme její skutečnou dráhu). Pravděpodobnostní vlny naší projekce se z obou štěrbin sčítají – a navzájem se v síti propojených intervalů opačných znamének ruší či posilují.

Interferenci po průchodu štěrbinami schematicky znázorňuje obr. 3.2.

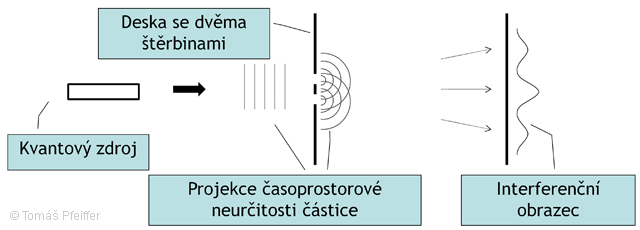
Obrázek 3.2: Vysvětlení dvouštěrbinového experimentu. Pokud dáme do cesty naší „projekci časoprostorové neurčitosti částice"desku se 2 štěrbinami, tato projekce projde oběma štěrbinami zároveň (a to se všemi důsledky včetně svého silového působení v obou místech současně). Za přepážkou se bude šířit dále, přičemž samotná pro nás nepozorovatelná částice stále nerozlišitelně kmitá mezi všemi možnými stavy kvantovaného časoprostoru (množinou vzájemně propojených intervalů opačného znaménka) . Nyní do vhodné vzdálenosti za dvouštěrbinovou přepážku umístíme stínítko. V důsledku nerozlišitelnosti se v místech dopadu částice musí potkávat interval kladného znaménka odpovídající průchodu jednou štěrbinou s intervalem kladného znaménka odpovídající průchodu druhou štěrbinou - proto dochází k interferenci a zesílení jen v určitých směrech v závislosti na vlnové délce a geometrii uspořádání.

Pokud však pomocí detektoru přímo pozorujeme, kterým otvorem prošla, pozorujeme částici zblízka = přesouváme pozici pozorovatele do jejího vlastního časoprostoru (!). V tu chvíli již pro nás částice není na horizontu poznání a platí pro ni klasická Newtonovská mechanika. Interferenční i ohybové vlnové projevy spojené s neurčitostí její projekce mizí.

Pokud bychom se v našem pozorování k částici přibližovali nikoliv skokově, ale postupně (představme si, že bychom se jednoduše zmenšovali – pozn.: uvažujeme objekt s nenulovou klidovou hmotností - k fotonům světla se takto přiblížit nemůžeme), pak by se částice v našem vjemu postupně zvětšovala a její klidová hmotnost by narůstala (důsledek zakřivení časoprostoru). Zároveň by se měnilo i časové měřítko našeho pozorování. Důsledkem této postupné změny parametrů - stále by platil vztah (3.1) λ = h/p = h/(mv) – by bylo i postupné zkracování vlnové délky λ dotyčné částice. Ta by se pak (tak jak by v našem pozorování opouštěla horizont poznání) stále více a více chovala podle klasické Newtonovské mechaniky.

Ve všem, co je kolem nás, můžeme pozorovat analogii - a v kvantové mechanice se nabízí analogie se zvlněním kapaliny. Nemusí přitom jít jen o klasické vlny na vodní hladině, například vědci Yves Couder a Emmanuel Forte z university „Paříž 7“ [33] a Daniel Harris z Massašutského Institutu Technologie [6] provedli experimenty, ve kterých použili kapku tekutiny poskakující v lázni vibrující kapaliny, poháněnou vlnami vznikajícími jejími vlastními kolizemi. Výsledný pohyb kapky, ač chaotický, byl přesně analogický pozorovanému chování kvantových částic.

A tak si vzhledem k časové i prostorové rozprostřenosti všech možných stavů, mezi kterými v našem pozorování částice zákonitě kmitá, můžeme představit, že zde svým způsobem dochází k rezonanci s okrajovými podmínkami danými uspořádáním experimentu, a funguje tak analogický „spojitý“ mechanismus, jako u kapky tekutiny popsaný v [33] a [6].

Námi vnímanou projekci částice si z pohledu vzdáleného pozorovatele můžeme představit jako chaotický oscilátor. Časoprostor se stává nelineárním rezonátorem, který „přebírá“ charakteristické fyzikální parametry oscilátoru a ovlivňuje jeho zdánlivý pohyb a výskyt. A tak zde máme zde uvedenou analogii s pohybem kapky v lázni vibrující kapaliny.

Vjemové rozvlnění časoprostoru nám tak může i připomínat dřívější teorie éteru, který do svých úvah zahrnovali již dávní řečtí filozofové [34].

Nyní se tak již můžeme podívat na to, zda by nám výše uvedená pozorování filozofie nemohla objasnit záhadu typických kvantových projevů mikrosvěta.