Kapitola 2

Filozofie Bytí

2.1 Horizont poznání

Zde předkládané filozofické vysvětlení soudobých vědeckých poznatků a záhad navazuje na filozofická pozorování a úvahy publikované v díle „BYTÍ – životní filozofie“ pana Josefa Zezulky¹[1] a v díle „Časoprostor + Gravitace“ [2], autor pan Tomáš Pfeiffer², který je žákem a pokračovatelem pana Zezulky.

Jak je známo z obecné teorie relativity [3] při popisu našeho vesmíru můžeme velmi dobře použít neeukleidovskou geometrii časoprostoru. V tomto pohledu je náš časoprostorový svět zakřivený, a dokonce v něm mohou existovat objekty, které nikdy nemůžeme přímo pozorovat – singularity, které zakřivují časoprostor natolik, že z nich neunikne ani světlo (známé „černé díry"³). Teorie černých děr definuje horizont událostí [21], za kterým jsou již všechny děje či události pro vnějšího pozorovatele nepozorovatelné.

Filozofickým pozorováním samotných základů našeho světa však můžeme pochopit zakřivení jako zcela základní a nedílnou vlastnost veškeré reality, ve které žijeme.

V důsledku tohoto zakřivení jsou naše možnosti pozorování vždy ohraničeny„horizontem poznání“ = mezní hranicí, za kterou již nemůžeme cokoliv vnímat.

Toto se týká nejen hmotného světa (tedy například kvantové mechaniky či astronomie), ale i všech jeho nehmotných aspektů, třeba psychologie, filozofie, historie, kultury, oblasti sociální, duchovní, zdravotní či jakékoliv jiné – prostě čehokoliv, co můžeme vnímat, pozorovat, hodnotit či jinak kvantifikovat.

Jde o zcela obecný zákon platný vždy a všude.

Z pohledu vědecké kvantifikace zde můžeme mluvit o hodnotě měřitelného intervalu, a vztahu k jeho skutečné velikosti v zakřiveném prostoru. Vztáhneme-li tento zákon například na problematiku mikro- a makrosvěta, můžeme zákon horizontu poznání schematicky znázornit dle obrázku 2.1 [2] Obrázek zdůrazňuje význam a důležitost průsečíku os x a y, který je místem pozorovatele⁴, a tedy i místem počátku intervalu.

Jak k tomu uvádí dílo Časoprostor + Gravitace [2], strana 8:

„Jako interval můžeme chápat cokoliv, co kvantifikujeme – vnímáme, měříme,hodnotíme, tedy cokoliv v našem světě. Týká se tedy matematiky, fyziky, astronomie, psychologie, filosofie, atd. Z obrázku vyplývá důležitost počátku osy, tedy místa počátku intervalu, tedy místa POZOROVATELE. (...) V blízkosti horizontu poznání již nepřidává jakkoliv velký interval v zakřiveném časoprostoru nárůst intervalu na fiktivní ose přímkové. Vzniká tak to, co nazývám (Tomáš Pfeiffer) horizontem poznání, za kterým již nelze cokoli pozorovat – měřit. To platí vždy oběma směry – směrem do vesmíru i do atomu, tedy pro světelné roky i angströmy. (...) Nelinearita se projeví i v tom, že pokus o kterékoliv měření je zatížen chybou, u malých intervalů nekonečně malou, a naopak u velkých nekonečně velkou.“ [2]

Naše schopnost pozorování mikro- i makrosvěta je tedy principiálně omezená. My totiž ve skutečnosti pozorujeme (a tedy i poměřujeme a kvantifikujeme) náš svět v rovině rovných pravoúhlých eukleidovských sítí. Jenže svět je ve skutečnosti zakřivený, a to tak, že u horizontu poznání ztrácíme schopnost cokoliv měřit, poznávat či kvantifikovat.

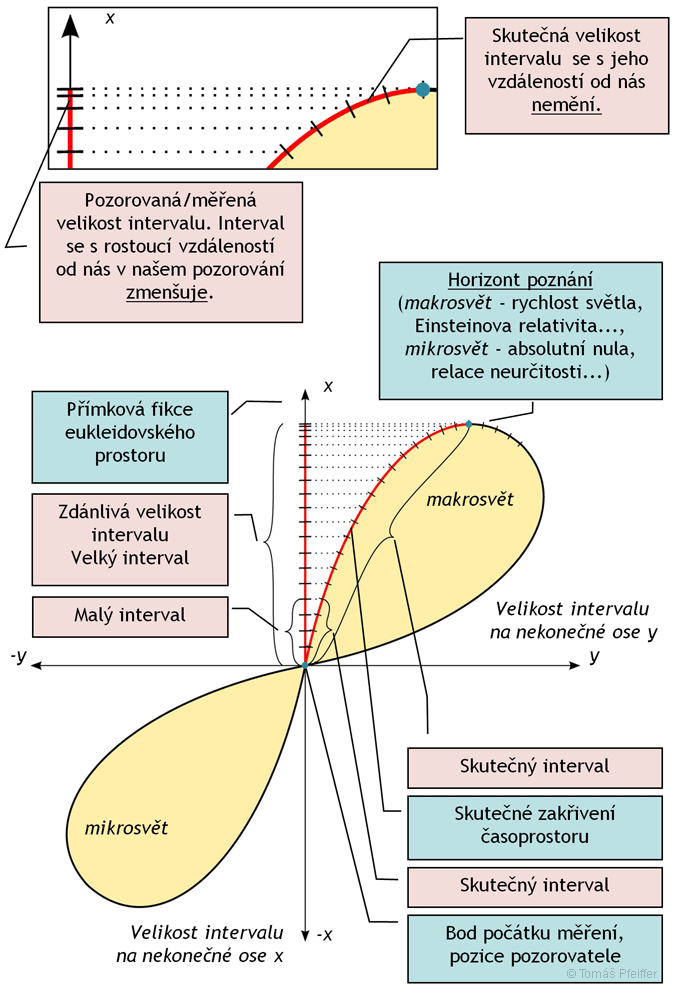
Obrázek 2.1: Horizont poznání [2] - schematické znázornění. „Na tomto obrázku je schematicky znázorněna závislost hodnoty měřitelného intervalu ve vztahu k jeho skutečné velikosti v zakřiveném prostoru. Tato závislost platí obecně do makro i mikrooblastí. V oblasti horizontu poznání je již nemožné určit pozici jako změnu velikosti intervalu. Vzniká neurčitost čehokoliv kvantifikovaného, tedy i prostoru a času.”

Náš vjem je v našem pozorování vždy lineární⁵.
Skutečný prostor (svět, vesmír) je vždy zakřivený⁶.
Proto existuje horizont poznání, za kterým již pozorovat nemůžeme.

A tak se nám intervaly při pohledu do mikrosvěta u horizontu poznání díky časoprostorovému zakřivení „natáčejí“, tedy se v našem lineárním vjemu zkracují a staví za sebe (jejich počet roste do nekonečna), a my díky tomu ztrácíme schopnost je jakkoliv měřit, kvantifikovat, rozlišovat mezi nimi.

Analogicky se nám přírůstky velkého intervalu (které jsou také intervaly) při pohledu do makrosvěta u horizontu poznání díky časoprostorovému zakřivení také „natáčejí“, tedy se v našem lineárním vjemu zkracují a staví za sebe (jejich počet roste do nekonečna), a my díky tomu ztrácíme schopnost je jakkoliv měřit, kvantifikovat, rozlišovat mezi nimi.

A tak můžeme stavět stále větší a větší urychlovače částic, můžeme konstruovat stále větší a větší dalekohledy a teleskopy – a přesto se (díky zakřivení) naše schopnost poznávat a pozorovat více bude stále snižovat (jak vyplývá z výše uvedeného grafu, další zvětšování intervalu na ose x již nebude znamenat nárůst naší schopnosti pozorovat skutečný interval v zakřiveném prostoru).

Z hlediska možnosti pozorovat a rozlišovat přitom není žádný rozdíl mezi pozorováním mikro- a makrosvěta.

V dnešní fyzice měříme a kvantifikujeme v metrech, Joulech a kilogramech (jde vlastně o fyzikální intervaly) – ale všechna tato kvantifikování jsou ve skutečnosti pouze lineárním měřením intervalu a závisí pouze na bodě, odkud pozorujeme, na naší pozici vzhledem ke zkoumanému objektu. Zákon horizontu poznání je proto klíčový i pro pochopení vztahu mikro- a makrosvěta [2], strana 14:

„Matematika velkých intervalů se velmi liší od té naší, lineární. Například doba života částice měřená v detektoru částic v urychlovači, například 10^-5s, reprezentuje ve skutečnosti milionleté intervaly v jejím časoprostoru, neb zákon relativity (horizontu poznání) platí na vše. Naměřené není tedy skutečnost, ale fikce lineárního zobrazení (...). Tytéž vztahy platí u částice též na stanovení její energie a hmotnosti.” [2]

Jak již uvedeno na obr. 1.2, měříme-li z našeho pohledu rozměry atomů v řádu10⁻¹¹až 10⁻¹⁰m, v časoprostoru dotyčného atomu může jít o rozměry v řádu10¹³až 10¹⁴m. Zatímco atom mikrosvěta může mít z našeho pohledu klidovou hmotnost v řádu 10⁻²⁷až 10⁻²⁶kg, z pohledu pozorovatele v mikrosvětě naměříme řádově například 10³⁰kg atd.

Horizont poznání si můžeme filozoficky představit jako dokonalou kouli, v jejímž středu stojí pozorovatel. Je v ní zcela uzavřen a tato koule mu znemožňuje pozorovat a poznávat cokoliv za svou hranicí. Pokud pozorovatel změní svou pozici (může se nejen posunout v prostoru, ale může se i zmenšit nebo zvětšit), celá koule se posune zároveň s ním.

Z pohledu relativity si můžeme představit i to, že se nepohybuje pozorovatel (ten zůstává stále stejný), ale zvětšuje či zmenšuje se svět kolem něj. Výsledný efekt je tentýž. Vždyť jsem-li ve člunu na řece, pohybují se břehy. Stojím-li na břehu, pohybuje se člun.

Změnu pozice/velikosti pozorovaného subjektu nám schematicky ukazuje obr. 2.2. Tento obrázek jen ilustruje to, že pojmy „menší“ a „vzdálenější“ jsou z pohledu myšlenek horizontu poznání vlastně zaměnitelné. Že „malé“ objekty mikrosvěta jsou pro naše pozorování právě tak „vzdálené“, jako vesmír jako celek.

Obrázek 2.2: Změna pozice/velikosti pozorovatele. Je človíček na obrázku stále menší a menší, nebo stále vzdálenější a vzdálenější?

¹ Pan Josef Zezulka je významným českým léčitelem a filozofem. Narodil se dne 30.3.1912. Ve věku svých 33 let (30.3.1945) zažívá nesmírně hluboký duchovní stav – „probuzení“. V tu chvíli se mění jeho vjem, chápání dějů, světa a rozšiřuje se jeho vědomí. Dostává dva dary: dar léčení a dar ducha. Díky nim nejen uzdravuje a zakládá léčitelský obor biotronika, ale začíná také předávat lidem nauku o základních životních pravdách – filozofii Bytí. Jeho jméno se postupně stává pojmem, a to i v mezinárodním měřítku.

² Pan Tomáš Pfeiffer je pokračovatelem pana Josefa Zezulky. Jako jeho žák nejen léčí a rozvíjí obor biotronika, ale na pravidelných přednáškách také předkládá a vysvětluje filozofii Bytí. Je otcem filozofické školy „Duchovní univerzita Bytí“ a zakladatelem „Společenství Josefa Zezulky“ – náboženské společnosti nového typu, pracující ku prospěchu celé biosféry. Více na www.dub.cz.

³ Černé díry jsou objekty s tak vysokou hmotností (tedy s tak silným gravitačním působením), že žádný objekt včetně světla nemůže jim odpovídající časoprostorovou oblast opustit. Černé díry byly teoreticky předpovězeny Obecnou teorií relativity [3], a jejich existence se dnes na základě astronomických pozorování bere za prokázanou.

⁴ Pod pojmem „pozorovatel“ zde chápeme jakoukoliv bytostnou/životní formu, která si uvědomuje svou existenci, „svůj pojem bytí – Já jsem“.  Pozorovatelem tak mohou být i zvířata, rostliny, či další možné životní formy.

⁵ Lineární závislosti či vztahy si můžeme představit jako závislosti, které lze matematicky popsat pomocí lineárních funkcí (kde se nevyskytují například mocniny apod.). Měřená výstupní hodnota je přímo úměrná hodnotě vstupní. Lineární funkci lze tedy napsat ve tvaru: f(x) = ax + b, kde a, b jsou libovolné konstanty

Můžeme si například představit, že čím delší bude cesta, tím více času na ní strávím (pokud půjdu stále stejnou rychlostí). Na (x) a f(x) se můžeme také dívat jako vztah příčiny a následku, tedy zde malá změna (x) způsobí malou změnu následku f(x). Geometrickým vyjádřením lineární veličiny je přímka. Změřením následku f(x) – třeba času strávenému na cestě - pak může nezávislý pozorovatel podat přesnou informaci o intervalu (x) – délce naší cesty.

⁶ Nelineární závislost (vyjadřující zakřivení) je závislostí, porušující výše uvedené. Pro vztah měřeného/pozorovaného výstupního intervalu f(x) veličiny k jejímu vstupnímu intervalu (x) již neplatí přímá úměra. Představme si, že na jednom místě nekonečné dlouhé ideálně rovné dálnice spolu stojí 2 lidé, člověk A a člověk B. B se rozeběhne, a bude se vzdalovat od pozorovatele A po této nesmírně dlouhé rovné cestě. Pozorovatel A si snadno zjistí jeho počáteční rychlost a uvidí jej jako postupně se zmenšující se postavičku. Jenže, čím delší bude cesta, tím více bude B unavený a poběží stále pomaleji a pomaleji. Čas strávený na cestě pak poroste s rostoucí délkou jeho cesty stále rychleji a rychleji. Při měření času, stráveného na cestě bude pro pozorovatele A majícího k dispozici pouze lineární časovou osu obtížnější přesně určit délku cesty, kterou B uběhl (poroste chyba jejího určení). Pokud by se B postupně vyčerpáním zpomaloval tak, že by se téměř zastavil, či začal dělat přestávky, je pro pozorovatele A, z měření času člověka B stráveného na cestě velmi obtížné či zcela nemožné zjistit skutečnou délku uběhlé trasy B. Pokud bude pozorovatel A předpokládat, že se mu B vzdaluje stále stejnou, konstantní rychlostí (tak jako na počátku, tedy uvažovat v eukleidovských osách), bude jeho zjištění (pozorování) zatíženo stále větší a větší chybou, rostoucí s rostoucí délkou cesty (intervalu) B.