Kapitola 3

Mikrosvět

3.4 Tunelování

Dalším typickým projevem kvantového světa je tunelování, díky kterému dokáže kvantová částice překonat i zdánlivě nepřekonatelnou překážku, jak znázorňuje obrázek 3.4.

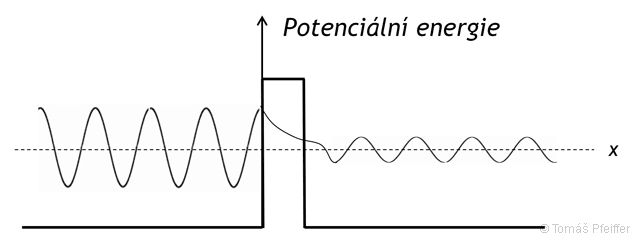
Obrázek 3.4: Tunelování. Rozdíl mezi klasickou a kvantovou mechanikou spočívá i v tom, že postavíme-li „klasickému“ hmotnému objektu do cesty bariéru s potenciální energií vyšší než je např. jeho kinetická či potenciální energie, objekt tuto bariéru nemůže překonat a odrazí se od ní (představme si například malou vzduchovou mezeru, či list papíru vložený mezi 2 různě nabitá vodivá tělesa). Naproti tomu kvantová částice může (v závislosti na vzájemném rozdílu energií a šířce bariéry) tuto překážku překonat a šířit se za ní beze ztráty energie dále (!). Jak je toto možné? I zde hraje roli pozice pozorovatele. Kvantování časoprostoru nelze ve vjemu vzdáleného pozorovatele omezit, vždyť pokud bychom toto dokázali, částice by se pro nás svým časoprostorovým projevem stala definovatelná a lokalizovatelná. To ovšem v důsledku existence horizontu poznání v principu není možné. Můžeme si představit, že i rozkmitání časoprostoru má svou časovou i prostorovou setrvačnost. Důkazem může být například to, že pokud bychom vhodným způsobem přidali do tohoto uspořádání citlivý kvantový detektor (podobně jako u dvouštěrbinového experimentu), tunelování by zcela zaniklo(!).

Proč může mít rozkmitání časoprostoru svou setrvačnost? Představme si částici (tedy v našem pozorování projekci časoprostorové neurčitosti bodu), která dorazí k potenciálové bariéře převyšující její energii. V tu chvíli dojde k rezonanci mezi částicí (naší projekcí) a bariérou, která v našem pozorování způsobí změnu vibrační charakteristiky časoprostoru jak na straně částice, tak i na straně samotné bariéry (časoprostor je jednota propojených intervalů, která za běžných okolností nemá diskontinuity). Samotná částice se však do bariéry nemůže dostat, a v našem pozorování se proto vyskytuje na „své“ straně bariéry. Její vibrační otisk se však díky rezonanci propojeného časoprostoru dostává i dovnitř bariéry (ve fyzice mluvíme o tzv. evanescentní vlně (viz např [36]), která je stojatá, svou fázi mění pouze podél bariéry ale nikoliv směrem do ní, a její amplituda směrem do bariéry exponenciálně klesá). Není-li bariéra příliš široká či vysoká (vzhledem k energeticko-vlnové charakteristice popisující naší projekci), může být tento vibrační otisk nenulový i na druhé straně bariéry. V tu chvíli dochází k dalšímu „předání“ tohoto otisku (z důvodu neexistence diskontinuity) a tedy kvantování časoprostoru i za bariérou. Naše projekce časoprostorové neurčitosti se tak může vyskytovat před i za bariérou (přeskakovat mezi intervaly před i za ní).

I v případě, kdy máme pouze jednu jedinou částici, tak můžeme pozorovat její projevy na obou stranách bariéry zároveň (stejně jako u průchodu oběma štěrbinami u dvouštěrbinového experimentu). Četnost výskytu kmitů (projevů) před a za bariérou se však navzájem liší a je dána uspořádáním experimentu.

I zde platí, že posunem pozorovatele k částici tunelové jevy zmizí.

Poslední experimenty (z roku 2015, viz [37]) prokazují, že je tomu skutečně tak. Vědci z Cornellovy university pozorovali, že atomy rubidia ochlazené na teplotu blízkou absolutní nule přestávají vykazovat jev tunelování a nechovají se dle Heisenbergovy relace neurčitosti, pokud je pozorujeme „zblízka“. Tento jev je také nazýván kvantový „Zenonův efekt“ – pozorujeme-li atomy přímo, nic kvantového se s nimi neděje. Jak jsme si již vysvětlili, jde o přímý důsledek přesunu pozorovatele k částici.

Můžeme se na totéž podívat i z pohledu zákona duality – každý zákon v sobě musí obsahovat i své porušení (jinak by nemohl existovat, tak jako nemůže existovat jeden magnetický pól bez druhého). Každá částice tak nutně musí mít i možnost projít skrze pro ni „nepřekonatelnou“ bariéru. Pozorovat tento jev v reálném světě „zblízka, tedy v jejím vlastním časoprostoru“ je však nemožné, k něčemu takovém dochází velmi, velmi zřídka. Při pozorování „zdálky“ je však vlastní čas částice vzhledem k pozorovateli natolik zrychlen, že tento jev zcela reálně zaznamenáváme jako tunelování. Posuneme-li pozorovatele k částici, do jejího času i prostoru (viz výše uvedený experiment, kdy ochlazením na teplotu blízkou absolutní nule „zpomalujeme“ i vlastní čas částice) – pak jej ale zcela zákonitě (vždyť v jejím vlastním čase toto zjevně nastává nesmírně zřídka) zaznamenat nemůžeme.